The pressure to prove one’s coding prowess can make a developer do some very clever and creative things with their source code. Sometimes it’s just a unique approach, but every once in a while this cleverness may shave a few milliseconds off of some performance metrics as well. In the end it’s not worth it. While this may seem like the type of innovation we want from our peers I’ve come to the conclusion it often does more harm than good. A quote that ran across my twitter feed a few weeks ago sums it up nicely: “So if you’re as clever as you can be when you write it, how will you ever debug it?” This pearl of wisdom comes from a book called “The Elements of Programming Style”. It’s a programming book from 1978 that is still entirely relevant. There’s a Wikipedia article you can check out if you’re not ready to take my word for it.
I know I’ve coded something in a unique fashion, and was quite sure I was being brilliant at the time, only to go back later and have absolutely no clue why I wrote the code the way I did. If I added comments I may be able to find my place again but sometimes it takes a while. What about when another developer runs into one of these bright ideas? Will any amount of meditation or contemplation allow them to make sense of what I was doing when I wrote it? Should a new or junior developer be expected to have some out of body experience before being able to work with me? Of course not. I hate it when I do this to myself, never mind when I run across someone else’s flash of genius. I certainly try to keep other devs from going through this type of mind freak as often as I can.
While this exercise can make for a fun parlor game and help extend our knowledge of the language we’re coding in it causes more problems than it solves in a team environment. A wiser developer sticks with a tried and true approach. They’ve been around long enough to know that the code needs to make sense to any garden variety developer that may be working with it in the future (which may in fact be the developer that wrote it in the first place).
I first learned this lesson years ago while tutoring mathematics. I had a developed an algorithm to generate the unit circle. Computer Science majors I was tutoring in math had an easier time using this to quickly generate the circle on scratch paper than arbitrarily memorizing it or understanding the standard proof that shows a bunch of triangles somehow morphing into a circle.
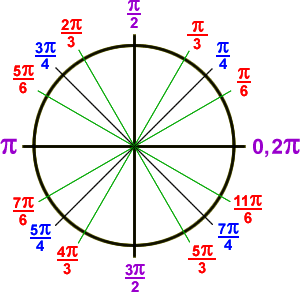
The algorithm requires a certain amount of seed data. One must know that a full circle is 2π radians in circumference. This puts the other quarter circle measures at π/2, π, 3π/4 respectively. Only a simple understanding of fractions is required to see this. Next we need to fill the first quadrant, which is only three more values, π/6, π/4, and π/3. From here the algorithm helps us extrapolate the remaining radian values for the circle.
First Quadrant: π/6, π/4, and π/3 (initial seed values, you have to remember these)
Second Quadrant: π – First Quadrant Corollary Value ( e.g., 3π/3 – π/3 = 2π/3, our 2nd quadrant value)
Third Quadrant: π + First Quadrant Corollary Value ( e.g., 3π/3 + π/3 = 4π/3, our 3rd quadrant value)
Fourth Quadrant: 2π – First Quadrant Corollary Value (e.g., 6π/3 – π/3 = 5π/3, our 4th quadrant value)
So, the formula for quadrants two through four can take the form of (n – s), (n + s), and (2n -s), where n = π and ‘s’ is one of the three seed values from the first quadrant. Three simple equations that any CS major should be entirely comfortable with using. There are a few other notes on this proof to get the coordinates, signs, and degree measurements correct. This is not a post about mathematics however, so I’ll leave that as a exercise for the more mathematically inclined to complete on their own time.
Other mathematicians where not as impressed as the CS majors and the student athletes were with this. Watching students that actively despised math struggle with memorizing the unit circle in an effort to complete their core was part of the fun of being good with numbers. It was suggested (by some troll of a jerk) that I might be a math noob myself, some poser that wasn’t any smarter than the fools he was tutoring. Impostor syndrome set in and I I felt I had no choice but to prove my mathematical prowess.
First I went big and reproved what I was doing with a Klien Four-Group. The trolls were quick to point out that this, like my first model, wasn’t a circle at all but just a bunch of points on a plane. Next I came back with a version using a rotational matrix. This did in fact generate a full circle with any value you like on it. The trolls had no more jabs for me but they also fell short of any compliment or encouragement for the work I had done.
As for the students I was helping, none of them quite understood the issue I had encountered. They viewed those trolls as nothing but trolls. Peers that only laughed at their struggle and refused to even try to help them. I ultimately found out my students were concerned that I had gotten sucked into this quagmire. The research I was doing was beyond their understanding and they were still using the first model I developed. It did exactly what they needed it to do. I was informed I should take the rising grades as evidence that my work was of merit and move on to a more productive use of my time and energy.
It was only then I noticed the trolls did have a point. The Klien Four-Group model and my original algorithm weren’t circles at all, just dots with values attached to them. A mathematician would have issue with this where a developer would not, since an object oriented developer should have a deeply rooted appreciation for abstraction. A class called Tree rarely resembles what we know to be a tree. It’s the use case that ends up being important. To a paper company a tree only needs to be represented by the amount of pulp they can expect it to produce. To an apple farmer it probably boils down to the number of apples the tree puts out and maybe its location in an orchard. What we take to be a tree, its size, the shape of its leaves, how it smells, the sound it makes when the wind catches it, are all details beyond the scope of most software we’ll ever write.
This happens to be a huge blocker for most new OOP developers, especially the ones that are good at math. The object model I was using to teach CS students how to do trigonometry ended up being the perfect tool to teach mathematicians how object oriented programming works. The rotational matrix version is important because sometimes non-standard values are needed. It’s useful to show how a method call may use standard values or extend onto another model, like the rotational matrix, when standard values don’t apply.
Mathematicians appreciate the Klien Four-Group model and I’m happy to show it off when I have the chance. More importantly, it’s a reminder to not get too fancy with math they’re putting into software. The math is beautiful more than it’s clever, and I’ve written code I feel the same way about. Like most works of art it stems from a hobby and should be left out of any applied scenario if it’s not practical. If we can get the same result with something that’s simple, something that’s easy to understand, easy to use, and even common, then that’s what we should use every single time because it will be easy to maintain. Wisdom is nothing more than knowledge applied over time. Time and time again I’ve come to the conclusion that maintainability trumps performance. We should be quick to sacrifice any minimal performance gain that makes our code difficult to understand. If a major performance gain is within reach then we’d be wise to abstract any strange code that was used to obtain it. I’d also advise you to comment the living day lights out of it as well, since you may need to remember how it worked yourself someday.



